With Raymond van Bommel, Edgar Costa, Noam D. Elkies, Sam Schiavone, and John Voight, we constructed an explicit polynomial with Galois group 17T7 (a split extension of \(\operatorname{Gal}(\mathbf{F}_{16}/\mathbf{F}_4) \cong C_2\) by \(\operatorname{PSL}_2(\mathbf{F}_{16})\) over the rationals: \[\begin{aligned} x^{17} &- 2 x^{16} + 12 x^{15} - 28 x^{14} + 60 x^{13} - 160 x^{12} + 200 x^{11} - 500 x^{10} + 705 x^{9} - 886 x^{8}\\ &+ 2024 x^{7} - 604 x^{6} + 2146 x^{5} + 80 x^{4} - 1376 x^{3} - 496 x^{2} - 1013 x - 490 \end{aligned}\]
The existence follows from the existence of a suitable Hilbert modular form \(f\). For the explicit polynomial, we construct the period lattice of the conjectural abelian variety of dimension \(4\) over a real quadratic base field \(F\) of \(f\). The \(2\)-torsion of that abelian variety realizes \(\operatorname{PSL}_2(\mathbf{F}_{16})\) over \(F\), and by Hilbert descent 17T7 over \(\mathbf{Q}\).
We assume the Eichler–Shimura conjecture (part of the Langlands philosophy) that one can attach an abelian variety \(A_f/F\) to \(f\) having isomorphic mod-\(2\) representations, and use some form of the BSD conjecture to construct the period lattice of \(A_f\). In the end, we quickly verify that our polynomial has Galois group 17T7 by a Magma computation.
The next smallest open case for the inverse Galois problem is the Mathieu group \(M_{23}\).
This is a follow-up to my blog entry from February 26, 2024. Mulun Yin (University of California Santa Barbara) managed to generalize our \(p\)-converse theorem for odd Eisenstein primes from the good ordinary to the potentially good ordinary case, i.e., allowing additive reduction at \(p\). Note that the construction of \(p\)-adic \(L\)-functions for additive \(p\) is an open problem in general.
The \(p\)-converse theorem (to the theorems of Gross–Zagier–Kolyvagin) states that in the situation above, if the \(p\)-Selmer rank \(r_p\) equals \(0\) or \(1\), then the analytic and algebraic rank equal \(r_p\).
One trick we are using is a proposition due to Nekovář that our modular form in question has an ‘untwist’ that has good reduction. Then we are using ‘Heegner pairs’ due to Jetchev–Loeffler–Zerbes (2021).
Together with results of Ari Shnidman et al. on the average \(3\)-Selmer rank in the presence of a \(3\)-isogeny, the result implies that the elliptic curve 13a3 (with a \(\mathbf{Q}\)-rational \(3\)-torsion point has \(\geq \frac{2}{3}\) of its quadratic twists satisfying the BSD rank conjecture.
The focus of the project [K–Stoll 2023] was the conjecture of Birch and Swinnerton-Dyer (BSD for short) for abelian surfaces. Abelian surfaces are two-dimensional abelian varieties, and abelian varieties are higher-dimensional analogues of elliptic curves. An elliptic curve is an algebraic curve that carries a group structure. This means that we can add two points on the curve to get another point on the curve, and this addition has similar properties as the standard addition. Elliptic curves are important in various contexts within mathematics, for example in the proof of Fermat’s Last Theorem or in cryptography.
Using the numbers of points modulo each prime number on an abelian variety \(A\) that is defined over the rational numbers, one can construct a certain function, the \(L\)-function of \(A\). The BSD conjecture for \(A\) proposes a surprising connection between the analytic behavior of the \(L\)-function of \(A\) and certain “global” invariants of \(A\). These invariants include properties of the group of rational points on \(A\) on the one hand and the number of elements of the mysterious Tate–Shafarevich group \(\mathrm{Ш}(A)\) of \(A\) on the other hand. Since all other quantities that occur in the conjecture can be computed for given \(A\), the conjecture can be expressed as “\(\mathrm{Ш}(A)\) is finite and has the expected number of elements”.
Birch and Swinnerton-Dyer originally formulated their conjecture for elliptic curves. To prove this version is one of the seven “Millennium Problems” of the Clay Foundation.
For general elliptic curves and even more so for higher-dimensional abelian varieties, the conjecture is wide open. It is not even known that \(\mathrm{Ш}(A)\) is always finite. For so-called “modular” abelian varieties with additional properties, some parts of the conjecture are known, however, in particular the finiteness of \(\mathrm{Ш}(A)\). Every elliptic curve defined over the rational numbers is modular, and so it was possible to verify the BSD conjecture for many individual elliptic curves. The goal of the project was to obtain the complete verification of the BSD conjecture also for many modular abelian surfaces. Except in cases that can be reduced to elliptic curves, this had not been done so far even for a single abelian surface. For the verification of the conjecture, we determined the size of \(\mathrm{Ш}(A)\).
The algorithms that we developed and the data on \(\mathrm{Ш}(A)\) are also useful outside the framework of this project.
We say that a number \(n \in \mathbf{Z}_{\geq 1}\) is a congruent number if there are \(x,y,z \in \mathbf{Q}\) such that \(y^2 = x^2 + n\) and \(z^2 = y^2 + n\), i.e., if the distance of successive numbers \(x^2,y^2,z^2\) is \(n\). (One can prove that \(n\) is congruent if and only if there is a right triangle with rational side lengths and area \(n\).)
Geometrically, we get an intersection of two surfaces of degree \(2\), and one can prove that the intersection is a plane cubic, e.g., the elliptic curve \(E\colon y^2 = x^3 - x\) from the blog entry from December 24, 2023.

The equation of the cubic can be can be computed using a computer algebra system like Magma.
What have we gained? We are in a situation where we have a lot of theoretical results and algorithms. Solutions to plane cubics \(E\) carry the structure of an abelian group \(E(\mathbf{Q})\), i.e., one can add points to get new ones. Furthermore, the theorem of Mordell (1922) says that the Mordell–Weil group \(E(\mathbf{Q})\) is finitely generated, i.e., that any solution can be obtained by adding finitely many points. Only because of this result, we can represent \(E(\mathbf{Q})\) in a computer!
Finite generation means that \(E(\mathbf{Q}) \cong E(\mathbf{Q})_\mathrm{tors}\times \mathbf{Z}^r\) for some (algebraic) rank \(r \geq 0\). It turns out that the finite torsion subgroup \(E(\mathbf{Q})_\mathrm{tors}\) is easily computed (there are only finitely many possibilities, see e.g. the blog entry from May 14, 2023), but it is a big unsolved open problem to compute \(r\). If one knows \(r\), one can compute a generating set of \(E(\mathbf{Q})\).
Conjecturally, one can compute \(r\) using the Birch–Swinnerton-Dyer conjecture: \[r = r_\mathrm{an}:= \operatorname{ord}_{s=1}L(E,s)\] Note that the analytic rank \(r_\mathrm{an}\) is an analytic and local invariant (more about this in a later blog entry), while the rank is algebraic and global in nature.
In algebra, one often has an equality (number we want to compute) \(=\) (number we can compute). It is more difficult here: We cannot compute both numbers individually, but assuming we know they are equal, we can compute both of them at the same time.
For example, this conjecture says that \(E(\mathbf{Q})\) is finite iff \(r = 0\) iff \(L(E,1) \neq 0\), and this is something computable (Cremona, Dokchitser). For example, the elliptic curve above has \(L(E,1) \approx 0.655514388573029952616209897473\), which proves that it is non-zero (note that a computation can show that an approximate complex number is non-zero, but proving equality to \(0\) is much harder!), hence \(E(\mathbf{Q}) = E(\mathbf{Q})_\mathrm{tors}\) is finite. One can easily prove that \(E(\mathbf{Q})_\mathrm{tors}\cong(\mathbf{Z}/2)^2\), and this implies that \(1\) is not a congruent number!
Another application is Fermat’s Last Theorem for the exponent \(n = 3\). One can compute that the equation \(x^3 + y^3 = z^3\) is equivalent to the elliptic curve \(E\colon y^2 = x^3 - 432\) and that \(r = r_\mathrm{an}= 0\). One has \(E(\mathbf{Q}) \cong\mathbf{Z}/3\), and this shows that the original equation only has trivial solutions \(xyz = 0\) over \(\mathbf{Q}\).
The Conjecture of Birch and Swinnerton-Dyer (“BSD” for short), originally formulated by Birch and Swinnerton-Dyer in the 1960s for elliptic curves over \(\mathbf{Q}\), is one of the most important open conjectures in number theory. For example, it is one of the seven “Millennium Problems”, for whose solution the Clay Foundation is offering a million dollars each. It relates in a surprising way analytic invariants of an elliptic curve \(E\), which are obtained via its \(L\)-series from its local properties (essentially the number of points modulo \(p\) on \(E\), for all prime numbers \(p\)), to global arithmetic invariants like the rank of the Mordell–Weil group \(E(\mathbf{Q})\), its regulator, and the rather mysterious Tate–Shafarevich group \(\mathrm{Ш}(E)\). The conjecture has been generalized to cover all abelian varieties over all algebraic number fields. It consists of two parts, which we will explain for the case of an abelian variety \(A\) of dimension \(g\) over \(\mathbf{Q}\).
One attaches to \(A\) its \(L\)-function \(L(A,s)\), which is defined by an Euler product over all prime numbers \(p\). If \(A\) is the Jacobian variety of a curve \(X\) of genus \(g\), the Euler factor at \(p\) for a prime \(p\) of good reduction is determined by the number of \(\mathbf{F}_{p^n}\)-points on the mod \(p\) reduction of \(X\) for \(n \leq g\). It follows from the Weil conjectures for varieties over finite fields that the Euler product converges for \(\operatorname{Re}(s) > \frac{3}{2}\) to a holomorphic function. A standard conjecture predicts that \(L(A,s)\) extends to an entire function; this is known when \(A\) is modular, i.e., occurs as an isogeny factor of the Jacobian \(J_0(N)\) of one of the modular curves \(X_0(N)\). By the Modularity Theorem of Wiles and others, this is always the case when \(A\) is an elliptic curve over \(\mathbf{Q}\) (this is now a special case of Serre’s Modularity Conjecture).
We now introduce the relevant global invariants of \(A\). By the Mordell–Weil Theorem, the abelian group \(A(\mathbf{Q})\) of rational points on \(A\) is finitely generated, so it splits as \(A(\mathbf{Q}) \cong A(\mathbf{Q})_\mathrm{tors}\oplus \mathbf{Z}^r\), where \(A(\mathbf{Q})_\mathrm{tors}\) is the finite torsion subgroup and \(r\) is a nonnegative integer, the rank of \(A(\mathbf{Q})\). There is a natural positive definite quadratic form \(\hat{h}\) on \(A(\mathbf{Q}) \otimes_\mathbf{Z}\mathrm{R}\cong \mathrm{R}^r\), the canonical height, turning \(A(\mathbf{Q})/A(\mathbf{Q})_\mathrm{tors}\) into a lattice in a euclidean vector space. The squared covolume of this lattice (equivalently, the determinant of the Gram matrix of \(\hat{h}\) with respect to a lattice basis) is the regulator \(\mathrm{Reg}_A\). The final global arithmetic invariant of \(A\) that we need is the Tate–Shafarevich group \(\mathrm{Ш}(A)\). It can be defined as the localization kernel \[\mathrm{Ш}(A) = \ker\Big({\text{\textup{H}}}^1(\mathbf{Q},A) \to \bigoplus_{v} {\text{\textup{H}}}^1(\mathbf{Q}_v,A)\Big)\] in Galois cohomology; here \(\mathbf{Q}_v\) denotes the completion of \(\mathbf{Q}\) with respect to a place \(v\) and the direct sum is over all places of \(\mathbf{Q}\). Geometrically, \(\mathrm{Ш}(A)\) is the group of equivalence classes of everywhere locally trivial \(A/\mathbf{Q}\)-torsors. This group is conjectured to be finite, but this is not known in general.
We also need some local invariants. To each prime \(p\), one associates the Tamagawa number \(c_p(A)\); this is the number of connected components of the special fiber at \(p\) of the Néron model \(\mathcal{A}/\mathbf{Z}\) of \(A\) and equals \(1\) for all primes of good reduction. Let \((\omega_1, \ldots, \omega_g)\) be the pull-back to \({\text{\textup{H}}}^0(A, \Omega^1)\) of a basis of the free \(\mathbf{Z}\)-module \({\text{\textup{H}}}^0(\mathcal{A}, \Omega^1)\) of rank \(g\). Then the real period of \(A\) is the volume of \(A(\mathrm{R})\) measured using \(|\omega_1 \wedge \dots \wedge \omega_g|\): \(\Omega_A = \int_{A(\mathrm{R})} |\omega_1 \wedge \dots \wedge \omega_g|\).
The weak BSD or BSD rank conjecture says that \(L(A,s)\) has an analytic continuation to a neighborhood of \(s = 1\) and \[r_\mathrm{an}:= \operatorname{ord}_{s=1} L(A, s) = r \,.\] The order of vanishing of \(L(A, s)\) at \(s = 1\) is also called the analytic rank of \(A\).
The strong BSD conjecture says that in addition \(\mathrm{Ш}(A)\) is finite and \[L^*(A,1) := \lim_{s \to 1} (s-1)^{-r} L(A, s) = \frac{\Omega_A \prod_p c_p(A) \cdot \mathrm{Reg}_A \#\mathrm{Ш}(A)}{\#A(\mathbf{Q})_\mathrm{tors}\#A^\vee(\mathbf{Q})_\mathrm{tors}} \,.\] Here \(A^\vee\) is the dual abelian variety; it is isomorphic to \(A\) when \(A\) is a Jacobian, or, more generally, when \(A\) is principally polarized.
Since all the other invariants of \(A\) can (usually) be computed at least numerically, we define the analytic order of Sha to be \[\#\mathrm{Ш}(A)_\mathrm{an}:= \frac{L^*(A,1)}{\Omega_A \mathrm{Reg}_A} \cdot \frac{\#A(\mathbf{Q})_\mathrm{tors}\#A^\vee(\mathbf{Q})_\mathrm{tors}}{\prod_p c_p(A)} \,.\] Assuming the BSD rank conjecture, strong BSD can then be phrased as “\(\mathrm{Ш}(A)\) is finite and \(\#\mathrm{Ш}(A) = \#\mathrm{Ш}(A)_\mathrm{an}\).”
Even the weak BSD conjecture for elliptic curves over \(\mathbf{Q}\) is wide open in general (this is the Clay Millennium Problem mentioned above). However, the strong BSD conjecture has been verified for many “small” elliptic curves; see below. The goal of the project [K–Stoll 2023] was to verify the strong BSD conjecture for the first time for a number of abelian surfaces \(A\), in a situation where it cannot be reduced to BSD for some elliptic curves. Concretely, this means that \(A\) is absolutely simple.
Let \(E/\mathbf{Q}\) be an elliptic curve of analytic rank \(0\) or \(1\) such that the mod-\(p\) Galois representation \(\rho_p\colon G_\mathbf{Q}\to \operatorname{Aut}(E[p](\overline{\mathbf{Q}}))\) is reducible (“Eisenstein prime”). In our recent preprint “On the anticyclotomic Iwasawa theory of newforms at Eisenstein primes of semistable reduction” with Mulun Yin (University of California Santa Barbara), we prove (a) the Iwasawa Main Conjecture and Perrin-Riou’s Heegner point Main Conjecture over a Heegner field in which the odd prime \(p\) of good or bad multiplicative reduction is split, as an application (b) a \(p\)-converse theorem (also for modular abelian varieties), and (c) the \(p\)-part of strong BSD if \(p > 2\) has good reduction.
Here are the elliptic curves \(E\) over \(\mathbf{Q}\) in the LMFDB with \(E(\mathbf{Q})_\mathrm{tors}\cong\mathbf{Z}/p\), rank \(0\) or \(1\), and \(p\) a prime of good reduction: \(p=3\), \(p=5\), and \(p = 7\).
As an application of (b), we obtain better proportions for the Goldfeld conjecture (\(50\,\%\) of the quadratic twists have rank \(0\) and \(50\,\%\) have rank \(1\)) for families of elliptic curves having a \(3\)-isogeny where \(3\) is a prime of good or bad multiplicative reduction. This follows from a combination with results of Ari Shnidman et al. on the average \(3\)-Selmer rank.
Let us now show that even our results on the \(p\)-part of strong BSD are for elliptic curves only (the reason is that [Jetchev–Skinner–Wan] for \(\rho_p\) irreducible work over imaginary quadratic fields that do not satisfy the Heegner condition), we can nevertheless use them to treat many more cases for modular abelian varieties with the article “Complete verification of strong BSD for many modular abelian surfaces over \(\mathbf{Q}\)” with Michael Stoll:
Consider the genus \(2\) curve \[X\colon y^2 = 5x^6 + 10x^5 - 13x^4 - 30x^3 + 9x^2 + 20x - 8\] with absolutely simple semistable RM Jacobian \(J\) of squarefree level \(5 \cdot 13\) and rank \(0\) associated to the newform 65.2.a.c. Note that this curves is not covered by op. cit. The algorithms from op. cit. prove the prime-to-\(3\) part of strong BSD for \(J/\mathbf{Q}\) with \(\#\mathrm{Ш}(J/\mathbf{Q})_\mathrm{an}= 2\). Our results allow us to also prove the \(3\)-part: Let the good ordinary prime \(3\) split as \(\mathfrak{p}\mathfrak{p}'\) in \(\mathbf{Z}[f]=\mathbf{Z}[\sqrt{3}]\) such that \(\rho_\mathfrak{p}\) is irreducible and \(\rho_{\mathfrak{p}'}\) is reducible with a trivial \(1\)-dimensional subrepresentation coming from the \(3\)-torsion. The results and algorithms of op. cit. prove that the Heegner index \(I_K\) for \(D_K = -131\) (so \(3\) is split in \(\mathcal{O}_K\)) equals \(\mathfrak{p}'\) times some ideal lying above \(2\), and that the Tamagawa product considered as an ideal in \(\mathbf{Z}[f]\) equals \(\mathfrak{p}'\). Hence [loc. cit., Theorem 5.2.2] proves that \(\mathrm{Ш}(J/\mathbf{Q})[\mathfrak{p}] = 0\). Our IMC (a) shows that \(v_{\mathfrak{p}'}(\#\mathrm{Ш}(J/K)[\mathfrak{p}'^\infty]) = 2v_{\mathfrak{p}'}(I_K) - 2v_{\mathfrak{p}'}(\operatorname{Tam}(J/\mathbf{Q})) = 2 - 2 = 0\). Since \(\mathfrak{p}' \nmid 2\), we have \(\mathrm{Ш}(J/K)[\mathfrak{p}'] \simeq\mathrm{Ш}(J/\mathbf{Q})[\mathfrak{p}'] \oplus \mathrm{Ш}(J^K/\mathbf{Q})[\mathfrak{p}']\), hence we get \(\mathrm{Ш}(J/\mathbf{Q})[\mathfrak{p}'] = 0\), so strong BSD holds for \(J/\mathbf{Q}\) with \(\mathrm{Ш}(J/\mathbf{Q}) \cong\mathbf{Z}/2\).
In our recent preprint “Complete verification of strong BSD for many modular abelian surfaces over \(\mathbf{Q}\)” Michael Stoll and I verify the strong Birch–Swinnerton-Dyer (BSD) conjecture for the first time for abelian surfaces over \(\mathbf{Q}\) in cases where it cannot immediately be reduced to elliptic curves, i.e., such that the surface is absolutely simple. Recall the conjecture for \(A/\mathbf{Q}\) a principally polarized abelian variety: \[L^*(A/\mathbf{Q},1) :=\lim_{s \to 1} (s-1)^{-r} L(A/\mathbf{Q}, s) = \frac{\Omega_A \prod_p c_p(A) \cdot \mathrm{Reg}_{A/\mathbf{Q}} \#\mathrm{Ш}(A/\mathbf{Q})}{(\#A(\mathbf{Q})_\mathrm{tors})^2} \,.\]
Assume the abelian surface is the Jacobian \(J\) of a genus \(2\) curve, with real multiplication, absolutely simple, and that the analytic rank of one of the newforms associated with it is \(0\) or \(1\). Then our Magma code can do the following:
Computation of the images of all residual Galois representations.
Computation of Heegner points and Heegner indices.
Formulas for the “analytic order of Sha”.
Euler system computations.
Isogeny descents.
Computations of approximations of \(p\)-adic \(L\)-functions.
Compute a finite set of primes for which one has to compute \(\mathrm{Ш}(J/\mathbf{Q})[\mathfrak{p}^\infty]\) to verify strong BSD. In practice, this set is small and often empty.
Assuming that one can compute the Mordell–Weil group of the abelian variety and heights, most of the algorithms generalize to modular Jacobians of any dimension.
Let me illustrate our algorithm with an example, the Jacobian of the genus \(2\) curve 4225.a.274625.1 of level \(N = 65 = 5\cdot13\) and rank \(0\).
All residual Galois representations at primes not above \(2\) or \(3\) are irreducible.
For the Heegner discriminant \(D = -51\), one gets the Heegner index \(2^2\cdot3\).
The analytic order of Sha is \(1\), as one can compute using modular symbols since the rank is \(0\).
The Euler system of Kolyvagin–Logachëv in an explicit version says that \(\mathrm{Ш}(J/\mathbf{Q})[\mathfrak{p}] = 0\) for \(\mathfrak{p}\nmid 2,3\): One always has to exclude the primes above \(2\), and additionally those dividing the Tamagawa product and the gcd of some Heegner indices, as well as those such that the residual Galois representation is reducible.
For the torsion prime \(\mathfrak{p}\) above \(3\), an isogeny descent shows that \(\mathrm{Ш}(J/\mathbf{Q})[\mathfrak{p}] = 0\).
No \(p\)-adic \(L\)-function is needed. In fact, for the “LMFDB examples”, we only use it for the curve with \(N = 188\).
One easily computes \(\mathrm{Ш}(J/\mathbf{Q})[2] = 0\) using existing algorithms in Magma. Hence \(\#\mathrm{Ш}(J/\mathbf{Q}) = 1 = \#\mathrm{Ш}(J/\mathbf{Q})_\mathrm{an}\).
I’m currently running our algorithms on all absolutely simple modular Jacobians associated with RM newforms with real quadratic coefficients up to level \(N \leq 1000\).
Our article has been accepted for publication in Forum of Mathematics, Sigma.
This is my first blog entry for the mathematically interested public.
My research interests lie in the field of number theory, especially arithmetic geometry. One studies properties of the natural numbers \(\mathbf{N}= \{0,1,2,\ldots\}\). One basic question is to ask for integral or rational solutions to systems of equations \(f_i(X_1, \ldots, X_n) = 0\) with \(f_i \in \mathbf{Z}[X_1,\ldots,X_n]\) polynomials in several variables. These are called Diophantine equations after Diophantus of Alexandria (maybe 250 AD). They define geometric objects, called varieties or schemes. These algebraic objects are investigated using both algebraic and geometric methods.
One of the reasons why we are interested in them is that finding their solutions is a easy-to-state problem, but solving them can be extremely hard and lead to significant and deep theoretical advances in number theory and related fields. An example for this is the solution of the 17th century Fermat equation \(a^n + b^n = c^n\), which required late 20th century mathematics. Number theory uses almost every other area of pure mathematics. Many mathematicians developed deep theories to tackle diophantine questions, and often one cannot easily see anymore what their connection to the original questions is. The abstract objects may even become more interesting that the originating equations.
However, the question whether a diophantine equation has an integral solution is undecidable (Hilbert’s 10th problem, theorem of Matiyasevich–Robinson–Davis–Putnam 1970). (There is no algorithm that enumerates the set of parameters of a parameterized diophantine equation for which there exists a solution.) Restricting the class of diophantine equations considered, the problem can or might be solvable, though. For example, it is solvable for (at most) quadratic equations, which follows from the Hasse–Minkowski theorem, a local-global principle. The class of curves, i.e., equations in only two variables is still open.
Aside from \(0\)-dimensional objects, which are algebraically also very interesting, the easiest objects are curves, i.e., \(1\)-dimensional objects. There is a discrete invariant of curves, called the genus. There are infinitely many “different” (i.e., non-isomorphic) curves of any genus \(g \geq 0\). In this blog entry, I will talk about the simplest ones, those of genus \(0\).
A classical example is the (projective) equation \[% \label{eq:PythagoreanTriples} X^2 + Y^2 = Z^2.\] By the Theorem of Pythagoras, its positive integer solutions correspond to right triangles with integral side lengths.
Excluding the trivial case \(Z = 0\) (because it implies \(X = Y = 0\) in integers) and dividing by \(Z\), we can equivalently determine the rational solutions to \(x^2 + y^2 = 1\) (with \(x = X/Z, y = Y/Z\)). Geometrically, the solutions to this equation form a circle:
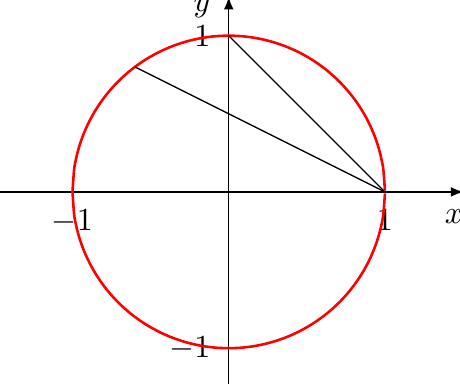
The integral solutions to the projective equation correspond to rational solutions to the affine equation (with the exception of the points at infinity). The algebraic question of finding solutions to the defining equation translates into the geometric question of finding points on the curve.
Now we do some geometry: There is one rational solution \((1,0)\), and if one draws a line through \((1,0)\) with slope \(t \in \mathbf{Q}\), this line intersects the circle in another point with rational coordinates (Bézout’s theorem—here we use that the equation has degree \(2\)), and all rational points can be obtained in this way. By calculating the coordinates of the intersection point, one gets an algebraic parameterization of the solutions: \[\begin{aligned} %\label{eq:Pythagorean parameterization} (x,y) = \Big(\frac{1-t^2}{1+t^2}, \frac{2t}{1+t^2}\Big), \quad t \in \mathbf{Q} \end{aligned}\] Reverting the process of dividing by \(Z\) again yields a parameterization of the original equation \[(X,Y,Z) = k(m^2 - n^2, 2mn, m^2 + n^2)\] with \(m,n,k \in \mathbf{Z}\). For example, letting \(m = 2, n = 1, k = 1\) yields the solution and most well-known Pythagorean triple \(3^2 + 4^2 = 5^2\).
More generally, plane quadrics (i.e., curves described by quadratic polynomials in two variables) \(ax^2 + by^2 = c\) belong to the simplest group of curves, those of genus \(0\). They have either no or infinitely many solutions, and there is a practical algorithm to decide what is the case. If there are infinitely many of them, one can parameterize them with one parameter \(t \in \mathbf{Q}\), as above.
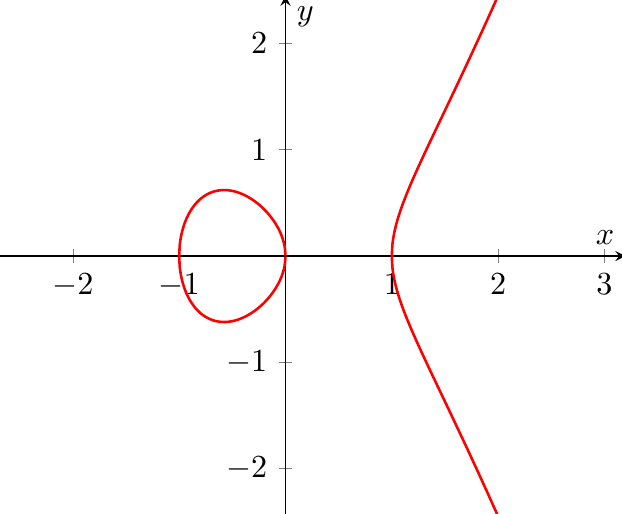
A more complicated example of a curve is the (affine) elliptic curve \[y^2 = x^3 - x\] with real picture:

It is a curve of genus \(1\). Its properties are better described by the complex points, which form a complex torus.
One can show that the only rational solutions are \((0,0),(\pm1,0)\). There are also elliptic curves with infinitely many points. Elliptic curves are much more complicated than plane quadrics, and several extremely deep conjectures, most notably the Birch–Swinnerton-Dyer (BSD) conjecture, have been formulated about them.
There is also a method, motivated by geometry, to generate new solutions out of old solutions. However, there is no simple geometric parameterization of all solutions anymore.
I will write more about elliptic curves in my next blog entry for the public.
Let \(E\) be an elliptic curve over \(\mathbf{Q}\). It is important to know for which primes \(p\) the mod-\(p\) Galois representation \(\rho_{E,p}: G_\mathbf{Q}\to \operatorname{Aut}(E[p](\overline{\mathbf{Q}})) \cong\operatorname{GL}_2(\mathbf{F}_p)\) is reducible. For example, this is the case when there is a non-trivial \(p\)-torsion point defined over \(\mathbf{Q}\). The irreducibility of \(\rho_{E,p}\) is an important condition for Euler systems (although we have partially removed this hypothesis in the appendix of [K–Yin 2024]) or in the modular approach to the (generalized) Fermat equation.
In his famous 1977 Eisenstein paper and a subsequent paper, Mazur classified all such primes for elliptic curves over \(\mathbf{Q}\). It turns out that the largest “Eisenstein prime”, i.e., a prime with \(\rho_{E,p}\) reducible for some \(E/\mathbf{Q}\) is \(163\), and it is \(37\) if \(E\) is not CM. The possible “torsion primes” \(p\) are \(\{2,3,5,7\}\).
The preprint Computing Quadratic Points on Modular Curves \(X_0(N)\) is joint work with Nikola Adžaga, Philippe Michaud-Jacobs, Filip Najman, Ekin Ozman, and Borna Vukorepa. We started to work on this at the 2022 MIT Modular curves workshop, whose aim was to extend the LMFDB with data on modular curves.
The \(\mathbf{Q}\)-rational points on \(X_1(N)\) and \(X_0(N)\) for all \(N\) have been computed by Mazur and Kenku. For the modular curve \(X_1(N)\) classifying (generalized) elliptic curves with a point of order \(N\), there is a bound \(N(d)\) by Merel and Kamienny such that \(X_1(N)(K)\) contains only cusps if \(N > N(d)\) and \(K\) runs through all number fields of degree \(d\). This has been used to compute all degree \(d\) points for \(d \leq 7\) by combined work of Kamienny–Kenku–Momose (\(d=2\)), Derickx–Etropolski–van Hoeij–Morrow–Zureick-Brown (\(d = 3\)), and for \(4\leq d\leq 7\) and prime values of \(N\) by Derickx–Kamienny–Stein–Stoll.
However, there is no \(d > 1\) such that one knows all degree-\(d\) points on \(X_0(N)\) (classifying elliptic curves with a cyclic \(N\)-isogeny) for all \(N\)! Conjecturally, the only quadratic points are cusps and CM points for \(N \gg 0\).
In our preprint, we improve on existing methods to compute quadratic points on modular curves and apply them to successfully find all the quadratic points on all modular curves \(X_0(N)\) of genus up to \(8\), and genus up to \(10\) with \(N\) prime, for which they were previously unknown. This extends previous work by Bruin–Najman, Ozman–Siksek, Box, and Najman–Vukorepa. Our methods apply to more than these curves; we restricted to these to make the computations feasible.
We use the following three methods:
Going down: If \(f\colon X \to Y\) is a finite morphism of curves and \(Y(K)\) is known and finite, one can compute \(X(K)\) by taking fibers. Problems arise if there are infinitely many quadratic points on \(Y\). We use this for \(N \in \{58, 68, 76 \}\).
Rank \(0\): If \(J_0(N)(\mathbf{Q}) = J_0(N)(\mathbf{Q})_\mathrm{tors}\) is known (we verify the generalized Ogg conjecture in several cases), one can compute the quadratic points on \(X_0(N)\) using a variant of the Mordell–Weil sieve. We use this for \(N \in \{ 80, 98, 100 \}\).
Atkin–Lehner sieve: This is the most involved method and a variant of the Mordell–Weil sieve, which, if applicable, reduces the problem to considering fixed points of an Atkin–Lehner involution and the rational points on a given Atkin–Lehner quotient. We use this for \(N \in \{ 74, 85, 97, 103, 107, 109, 113, 121, 127 \}\).
We also give optimized algorithms to compute models of Atkin–Lehner quotients of \(X_0(N)\) and the \(j\)-invariant morphism.
Note that there can be infinitely many quadratic points on a curve \(X\); this happens if and only if \(X\) is hyperelliptic (plug in infinitely many values for \(x\) in \(y^2 = f(x)\)) or bielliptic with elliptic curve of rank \(> 0\).
We get evidence for the fact that non-cuspidal, non-CM points are rare.
Here are my slides for a talk at a conference in Dubrovnik.
The article has been accepted for publication in Mathematics of Computation.
Recently, two articles have been accepted:
In Quadratic Chabauty for Atkin-Lehner Quotients of Modular Curves of Prime Level and Genus 4, 5, 6 (with Nikola Adžaga, Vishal Arul, Lea Beneish, Mingjie Chen, Shiva Chidambaram, and Boya Wen), accepted for publication in Acta arithmetica, we apply the quadratic Chabauty method to determine all \(\mathbf{Q}\)-rational points of Atkin–Lehner quotients \(X_0(p)^+\) of prime level \(p\) such that the genus is in \(\{4,5,6\}\).
Since the non-cuspidal points of \(X_0(p)\) correspond to elliptic curves with a \(p\)-isogeny and since the Atkin–Lehner (or Fricke) involution \(w_p\) maps such an isogeny to its dual, our result classifies elliptic curves with an unordered pair of \(p\)-isogenies. Computing the points on \(X_0(p)^+ := X_0(p)/w_p\) has been called an “extremely interesting arithmetic question” by Mazur in his seminal Eisenstein paper. For composite levels \(N\), one can mod out (potentially) more Atkin–Lehner involutions and go down to the quotient \(X_0(N)^*\). The \(\mathbf{Q}\)-points on the hyperelliptic \(X_0(N)^*\) have been determined in our ANTS paper, see my blog post from August 12, 2022 below.
Our article proves a conjecture of Galbraith for those curves. The main difficulty in computing the set of rational points was to find suitable plane models of those modular curves such that the existing implementation of the Quadratic Chabauty algorithm determined the set of rational points. It was surprising to the experts that we could go up to (relatively high) genus \(6\). This article originated from a project started at the 2020 Arizona Winter School.
Those of smaller genus have been tackled before, for example in the article Quadratic Chabauty for modular curves: Algorithms and examples by Balakrishnan–Dogra–Müller–Tuitman–Vonk. Those of composite level and genus \(\leq 6\) are known known by work of Momose with \(X_0(125)^+\) being solved in Arul–Müller.
In Specialization of Mordell-Weil ranks of abelian schemes over surfaces to curves, accepted for publication in International Journal of Number Theory, I prove the following surjectivity result for specialization morphisms: Recall that Silverman’s specialization theorem (with generalizations by Wazir) roughly says that for an abelian variety \(A\) over a function field \(K\) over a global field, outside a set of bounded height, the specialization theorem from the Mordell–Weil group \(A(K)\) to the Mordell–Weil group to closed points is injective modulo torsion, i.e., the rank does not drop.
It is a challenging question whether there exist infinitely many specializations that the rank does also not jump! For example, when applied to a family of elliptic curves over \(\mathbf{Q}(T)\) with generic rank \(r\) (such families exist for small \(r\)), a positive answer to this question would imply that there are infinitely many non-isomorphic elliptic curves over \(\mathbf{Q}\) with rank exactly equal to \(r\). The latter is known for \(r = 0,1\) (explicit constructions or the Gross–Zagier formula combined with Kolyvagin’s Heegner point Euler system), but open already for \(r = 2\).
My article does not solve this question, but shows that for an abelian scheme over a surface, infinitely many specializations to curves have the same rank.
The proof uses a recent result of Ambrosi on a specialization theorem of Néron–Severi ranks and the Shioda–Tate formula to go from Néron–Severi ranks to Mordell–Weil ranks. The result holds more generally over infinite finitely generated fields.
My original motivation to prove such a result was to prove the reduction of the analog of the Birch–Swinnerton-Dyer conjecture over higher-dimensional bases to that over curves, with the reduction to surfaces as a basis established in my Documenta article and the reduction to curves by my recent article.
I have been back to Bayreuth to my quadratic Chabauty conference (it had to take place there because of my funding).
We had three remote working groups, one in the US and two in Europe, working on ongoing projects. Five of us worked in person starting something new. We will continue working on our problems after the conference.
Here are the slides of my 25 minutes talk I gave at ANTS-XV (Fifteenth Algorithmic Number Theory Symposium), taking place at the University of Bristol this year. This is the largest international conference on this topic.
I talked about the completion of the determination of the \(\mathbf{Q}\)-points on the Atkin-Lehner quotients \(X_0(N)^*\) which are hyperelliptic. There are exactly \(64\) of them, and they were determined by Hasegawa in 1997. Here is our paper and our Magma code with log files.
To do this, we used a combination of well-established (Chabauty–Coleman method in its implementation by Balakrishnan–Tuitman, elliptic curve Chabauty in its implementation by Bars–González–Xarles) and recent developments in the quadratic Chabauty method by Balakrishnan–Dogra–Müller–Tuitman–Vonk.
Looking at the root number, you expect that most \(X_0(N)^*\) with \(N\) square-free have \(r = g\) (\(g\) the genus of the curve and \(r\) the Mordell-Weil rank of its Jacobian \(J\)) because the corresponding space of cusp forms is \(S_2(\Gamma_0(N))^{w_d = +1 : d \mid N, (d,N/d)=1}\), so the analytic ranks of the \(L(f,s)\) are odd and in fact should conjecturally be \(1\) in most of the times. In these cases, the Chabauty–Coleman method will not be applicable (except if the \(\mathbf{Z}_p\)-rank of the closure of \(J(\mathbf{Q})\) in \(J(\mathbf{Q}_p)\) will be less than \(g\)), and you need quadratic Chabauty.
As David Harvey asked, we usually have many fake residue discs coming from the various Chabauty methods. These need to be ruled out using the Mordell-Weil sieve. For genus \(g > 2\), one would not expect fake residue discs from quadratic Chabauty (in fact, we didn’t have this problem in our genus \(4,5,6\) paper) because there are more Chabauty functions if \(g-1 = \operatorname{rk}\, \mathrm{NS}(J) - 1 \geq 2\). If there are, there should be a geometric reason explaining them.
We (Nikola Adžaga, Shiva Chidambaram, Oana Padurariu, and me) and others will work on non-hyperelliptic \(X_0(N)^*\) and on quotients of Shimura curves on my conference in two weeks.
This is the first entry of my blog started as announced in my Marie Skłodowska-Curie fellowship starting in June 2023 with Steffen Müller in Groningen.
It is the end of the second week at PCMI “Number Theory Informed by Computation” organized by the Princeton Institute of Advanced Study, which I enjoy very much. I could continue many collaborations and start new ones, for example with Ross Paterson and Carlo Pagano. When there are preprints available at arXiv, I will write a blog post here.
Here are the slides of my 25 minutes talk I gave in the Research Program. The talk was about the exact verification of the strong Birch–Swinnerton-Dyer (BSD) conjecture for some abelian surfaces with real multiplication over \(\mathbf{Q}\). There were several interesting questions by Levent Alpöge, Sam Frengley, Bjorn Poonen, and Akshay Venkatesh. For example, I hope I can prove strong BSD for an example of a Jacobian of a genus \(2\) curve of level \(3200\) provided by Sam, which has rank \(0\) and \(7\)-torsion in the Shafarevich–Tate group. (All examples I computed had order of Sha equal to \(1,2,4\).) Akshay suggested to formulate a refinement of an equivariant BSD formula. I did so over Heegner fields and I will check whether this formula holds in my examples. The question of Levent was about the Galois representations, and Bjorn asked for an heuristic explanation why the Shafarevich–Tate group is trivial for all Atkin-Lehner quotients with Jacobian absolutely simple and modular of dimension \(2\).
After the third week, I’m at ANTS-XV, where I will give a talk about our paper on the determination of the \(\mathbf{Q}\)-points on hyperelliptic Atkin-Lehner quotients of modular curves accepted there.
As the audience of this blog is also the interested mathematical public, I will post some introductory entries on curves and abelian varieties besides the research topics.
If you have a comment, please e-mail me and I will publish it
here. I do not want to have additional active code running on my server
or deal with spammers.
Impressum Datenschutzerklärung